In this post, we will see what Big O notation is and how to use it to optimize our algorithms.
But first of all, what is Big O notation?
From Wikipedia:
“Big O notation is a mathematical notation that describes the limiting behaviour of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for Ordnung, meaning the order of approximation.
In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; a famous example of such a difference is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates.“
In a nutshell, the Big O notation is used to describe the performance or complexity of an algorithm relative to the size of the input.
It will help us to understand the worst-case complexity of an algorithm and it gives us a high-level sense of which algorithms are fast, which are slow and what the trade-offs are.
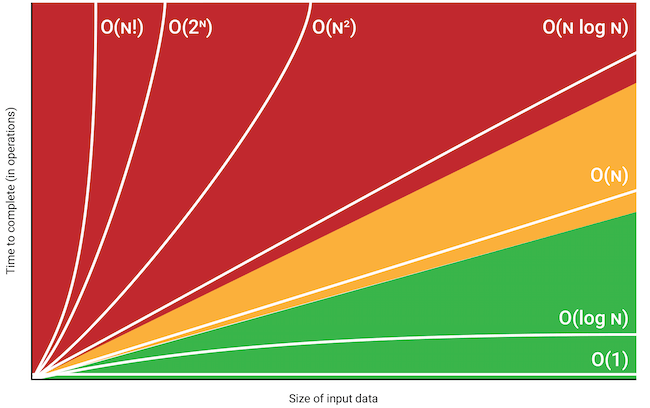
The four algorithms that we will see in this post are (from best to worst):
Constant algorithm: O(1)
Linear algorithm: O(n)
Quadratic algorithm: O(n^2)
Exponential algorithm: O(2^n)
First of all, we create a .net Console Application called BigONotation and then, using the command
Install-Package BenchmarkDotNet
we install the BenchmarkDotNet library.
Then, we create a Class called CoreAlgorithms that we will use to create four methods for testing the algorithms.
Finally, we will create another Class called BenchmarkCore used to run the benchemarks for the methods in CoreAlgorithms.
The BenchmarkCore Class will be called from the Program.cs file.
CONSTANT ALGORITHM [O(1)]
In this case the processing time is independent from the input:
[COREALGORITHMS.CS]
namespace BigONotation;
public class CoreAlgorithms
{
public decimal ConstantAlgorithm(int valueInput)
{
return valueInput / 2;
}
}
[BENCHMARKCORE.CS]
using BenchmarkDotNet.Attributes;
namespace BigONotation;
[MemoryDiagnoser]
[Orderer(BenchmarkDotNet.Order.SummaryOrderPolicy.FastestToSlowest)]
[RankColumn]
public class BenchmarkCore
{
private CoreAlgorithms? objCore;
[GlobalSetup]
public void GlobalSetup()
{
objCore = new CoreAlgorithms();
}
[Arguments(1)]
[Arguments(10)]
[Arguments(100)]
[Arguments(1000)]
[Arguments(10000)]
[Arguments(100000)]
[Arguments(1000000)]
[Benchmark]
public void CheckConstantAlgorithm(int valueInput)
{
objCore.ConstantAlgorithm(valueInput);
}
}
[PROGRAM.CS]
using BenchmarkDotNet.Running;
using BigONotation;
Console.WriteLine("Start Benchmark");
BenchmarkRunner.Run<BenchmarkCore>();
If we run the benchmarks, this will be the result:

LINEAR ALGORITHM [O(n)]
In this case the performance will grove linearly to the size of the input.
[COREALGORITHMS.CS]
namespace BigONotation;
public class CoreAlgorithms
{
public bool LinearAlgorithm(int numberOfItems, int valueInput)
{
var lstValue = Enumerable.Range(1, numberOfItems).ToList();
foreach (var item in lstValue)
{
if(item == valueInput)
return true;
}
return false;
}
}
[BENCHMARKCORE.CS]
using BenchmarkDotNet.Attributes;
namespace BigONotation;
[MemoryDiagnoser]
[Orderer(BenchmarkDotNet.Order.SummaryOrderPolicy.FastestToSlowest)]
[RankColumn]
public class BenchmarkCore
{
private CoreAlgorithms? objCore;
[GlobalSetup]
public void GlobalSetup()
{
objCore = new CoreAlgorithms();
}
[Arguments(1000,500)]
[Arguments(10000, 5000)]
[Arguments(20000, 10000)]
[Arguments(50000, 25000)]
[Arguments(100000, 50000)]
[Arguments(200000, 100000)]
[Benchmark]
public void LinearAlgorithm(int numberOfItems, int valueInput)
{
objCore.LinearAlgorithm(numberOfItems, valueInput);
}
}
If we run the benchmarks, this will be the result:

QUADRATIC ALGORITHM [O(n^2)]
In this case the performance will grow linearly and in direct proportion to the size of the input squared.
We take the previous method for the Linear Algorithm and we will add another loop; we will see that the Mean will be the double of the Linear Algorithm method.
[COREALGORITHMS.CS]
namespace BigONotation;
public class CoreAlgorithms
{
public bool QuadraticAlgorithm(int numberOfItems, int valueInput)
{
var lstValue = Enumerable.Range(1, numberOfItems).ToList();
var lstValue2 = Enumerable.Range(1, numberOfItems).ToList();
foreach (var item in lstValue)
{
foreach (var item2 in lstValue2)
{
if (item2 == valueInput)
return true;
}
}
return false;
}
}
[BENCHMARKCORE.CS]
using BenchmarkDotNet.Attributes;
namespace BigONotation;
[MemoryDiagnoser]
[Orderer(BenchmarkDotNet.Order.SummaryOrderPolicy.FastestToSlowest)]
[RankColumn]
public class BenchmarkCore
{
private CoreAlgorithms? objCore;
[GlobalSetup]
public void GlobalSetup()
{
objCore = new CoreAlgorithms();
}
[Arguments(1000,500)]
[Arguments(10000, 5000)]
[Arguments(20000, 10000)]
[Arguments(50000, 25000)]
[Arguments(100000, 50000)]
[Arguments(200000, 100000)]
[Benchmark]
public void QuadraticAlgorithm(int numberOfItems, int valueInput)
{
objCore.QuadraticAlgorithm(numberOfItems, valueInput);
}
}
If we run the benchmarks, this will be the result:

EXPONENTIAL ALGORITHM [O(2^n)]
In this case the performance will grow doubles with each addition to the input data set.
With a small input the growth is very small but, when the input gets larger, the performance rises exponentially.
An example of this algorithm is the calculation of the n-Fibonacci number.
[COREALGORITHMS.CS]
namespace BigONotation;
public class CoreAlgorithms
{
public long ExponentialAlgorithm(int valueInput)
{
if (valueInput <= 1)
return valueInput;
return ExponentialAlgorithm(valueInput - 1) + ExponentialAlgorithm(valueInput - 2);
}
}
[BENCHMARKCORE.CS]
using BenchmarkDotNet.Attributes;
namespace BigONotation;
[MemoryDiagnoser]
[Orderer(BenchmarkDotNet.Order.SummaryOrderPolicy.FastestToSlowest)]
[RankColumn]
public class BenchmarkCore
{
private CoreAlgorithms? objCore;
[GlobalSetup]
public void GlobalSetup()
{
objCore = new CoreAlgorithms();
}
[Arguments(1)]
[Arguments(2)]
[Arguments(3)]
[Arguments(4)]
[Arguments(5)]
[Arguments(6)]
[Arguments(7)]
[Arguments(8)]
[Arguments(9)]
[Arguments(10)]
[Arguments(11)]
[Arguments(12)]
[Arguments(13)]
[Arguments(14)]
[Arguments(15)]
[Arguments(16)]
[Arguments(17)]
[Arguments(18)]
[Arguments(19)]
[Arguments(20)]
[Benchmark]
public void ExponentialAlgorithm(int valueInput)
{
objCore.ExponentialAlgorithm(valueInput);
}
}
If we run the benchmarks, this will be the result:
